Tolkien's Legendarium versus Astronomical Reality
or: Just how unskilled is Tolkien in these matters?
by Aaron Chong
Version 0.9721 (published 2016-03-05)
At first glance the attention to chronology and time in Lord of the Rings is quite impressive. Lunar phases seem to be consistent throughout the narrative, calendars have been worked out in detail, even including adjustments for the drift with respect to the solar year. From this basis many have attempted to extend the calendars in the story to the present day, and more than one have claimed to be able to pin down the exact date of the destruction of the Ring. However, with a sufficient level of astronomical knowledge it is quickly seen that many of the assumptions Tolkien made are invalid, which turns matching the chronology with actual history into a complete mess. This article will explain why and attempt to find some ways to remedy this matter. As a "bonus" it also contains a new proposed chronology for The Hobbit.
Preface: Some technical points (notation, etc.)
In this article I will use ISO 8601 notation (yyyy-mm-dd, astronomical year numbering, proleptic Gregorian calendar) for dates in general. Julian calendar dates will be denoted with slashes, and use CE/BCE year labels excluding 0. In addition, I will also use the Julian day (JD) and Julian day number (JDN, here defined as round(JD)); the Julian day count is defined such that noon GMT (as UTC did not exist then) at 4713 BCE/01/01 (-4713-11-24) equals 0.
For dates in the various Middle-earth calendars the original forms as supplied by Tolkien will be used (Quenya for Calendar of Imladris and Kings'/Steward's/New Reckoning, Anglicised Northern Mannish (Westron?) for Shire Reckoning). Years will be denoted by a Roman numeral for the age followed by the year number, separated by a single period. The periods of the First Age will be distinguished by a letter in brackets e.g. I(s).590 for the 590th Year of the Sun of the First Age, though only the Years of the Sun are used in the text. Shire Reckoning will be denoted by the letters SR (Bree's reckoning is not used in the text).
Finally, it should be noted that my printed source is a Hobbit/LotR box set dating from the early 2000s and corresponding to editions from the 1990s. There are a few relevant corrections in more recent editions, which will be pointed out in the text where they come up; conversely, the first edition also has a few relevant alterations. Most of these are obtained via the Reader's Companion.
Part 1: An overview of the calendars in Lord of the Rings, and their structure
There are five calendars that are described in sufficient detail to be implemented in Lord of the Rings, specifically Appendix D (Time and Calendars, sometimes abbreviated to TC as in Andreas Möhn’s work). (The dwarves used some form of lunar or lunisolar calendar in the past, as mentioned in The Hobbit; however, no details of its structure apart from Durin's Day are given. In addition, the Prologue mentions Merry publishing relationships between Shire Reckoning and the calendars of Imladris, Gondor and Rohan; it is not specified whether the last referred to an independent calendar.) This section will give an overview of their main features. In addition, this section will also cover the calendars supplied in History of Middle-earth part 12 (Peoples of Middle-earth).
Most of the information found in this section can be found in many online sources - for example, Möhn, Shapiro, Three Rings, as well as Baker etc. all address the topic. The exception is the calendars from PoME, which do not seem to be described in implementation-level detail on any other websites.
1a: The Calendar of Imladris
The first of the calendars described is the Calendar of Imladris, or the Reckoning of Rivendell. (Annals of Ennor claims that it was not actually used by Imladris, however a source for this is not cited and so this should be considered apocryphal.) A solar year was referred to as a coranar ("sun-round") when considered astronomically or as a loa ("growth") when considered with respect to the seasons; since we are working astronomically we will use the first term. The largest unit of this calendar was the yén, which equals 144 coranari. Each coranar contained six seasons, known in Quenya as tuilë, lairë, yávië, quellë (lasse-lanta), hrívë, coirë and in Sindarin as ethuil, laer, iavas, firith (narbeleth), rhîw, echuir. In English the names translate roughly to spring, summer, autumn, fading (leaf-fall), winter and stirring. The second and fifth of these seasons had 72 days and the remainder had 54. In addition there were five days outside the seasons (eight in leap years): yestarë ("first-day", before the first season), three enderi ("middle-days", six in leap years) between the third and fourth seasons, and mettarë ("last-day", after the last season). Thus, the coranar contained 365 or 368 days. Leap years were every twelfth coranar of the yén excepting the last coranar of every third yén, hence the yén contained 52596 or 52593 days. The adjustment of any other inaccuracy is unknown; I will later show that most likely there was no such adjustment between the start of the Second Age and the end of the Third Age.
The Eldar also observed an enquië (week) of 6 days, reckoned continuously. The names of the weekdays were in Quenya Elenya, Anarya, Isilya, Aldúya, Menelya and Valanya (Tárion), and in Sindarin Orgilion, Oranor, Orithil, Orgaladhan, Ormenel and Orbelain (Rodyn). These roughly translate to English as Starday, Sunday, Mo(o)nday, Treesday, Heavensday and Valarday.
The epoch of the calendar is unknown, however it is known that yestarë in III.3019 corresponded to 6 Astron (5 Víressë Stewards' Reckoning, 11 Víressë (proleptic?) New Reckoning). This provides difficulties when attempting to determine day intervals, since the analysis could be out by three days in either direction.
Some secondary sources (Shapiro, Annals of Ennor) have also claimed that the beginning of an Age would result in a new yén, truncating the previous one. This is probably not true, since if this had happened during the writing of the Red Book surely it would have been mentioned. (Had the Third Age lasted three years longer then the next enderi doubling would also have been skipped; this is not mentioned either.)
The average length of a coranar is 365+3/12-3/432 = 365+35/144 = 365.24305̅ days, or 365 days 5 hours 50 minutes exactly. This compares somewhat favourably with modern calendars.
1b: Kings' Reckoning
The Kings' Reckoning (spelt King's until 2005) was the calendar used in Númenor. It divided the year into 12 astar (months), named Narvinyë, Nénimë, Súlìmë, Víressë, Lótessë, Náríë, Cermië, Urimë, Yavannië, Narquelië, Hísimë, Ringarë in Quenya or Narwain, Nínui, Gwaeron, Gwirith, Lothron, Nórui, Cerveth, Urui, Ivanneth, Narbeleth, Hithui, Girithron in Sindarin. Each had 30 days except the sixth and seventh which had 31. In addition there were three days outside the months (four in most leap years), yestarë before the first month, loëndë between the sixth and seventh months (replaced by two enderi in leap years), and mettarë after the last month.
Leap years were every fourth year excepting years divisible by 100; Tolkien mentioned the term haranyë but his wording makes it unclear as to whether it refers to the whole 100-year period or the last year of the period. In addition, adjustments were made in years divisible by 1000, but their nature is not stated explicitly in TC. However, noting that Tolkien's calculation of the millennial deficit is 4 hours 46 minutes 40 seconds and is based on a year length of 365 days 5 hours 48 minutes 46 seconds exactly, we conclude that years divisible by 1000 were double-leap years, thus containing three enderi (for more detail, refer to part 2). (I have since found that the first edition explicitly stated that the millennial additions were 2 days in length.)
The average length of a Númenorean year is then 365 + 1/4 - 1/100 + 2/1000 = 365.242 days exactly, or 365 days 5 hours 48 minutes 28.8 seconds. This is confirmed by Tolkien in letter 176 (1955-12-08), which also claims that the calendar is more accurate than the Gregorian calendar (365+97/400 = 365.2425 days exactly, or 365 days 5 hours 49 minutes 12 seconds). More on this supposed superiority later, in part 4.
The weekdays were mostly the same, except that the Treesday (Aldúya/Orgaladhan) was altered to singular (Aldëa/Orgaladh), and at some point in the Second Age a "Seaday" (Eärenya/Oraeron) was added, making the weekdays in Quenya Elenya, Anarya, Isilya, Aldëa, Menelya, Eärenya and Valanya (Tárion), and in Sindarin Orgilion, Oranor, Orithil, Orgaladh, Ormenel, Oraearon and Orbelain (Rodyn).
1c: Shire Reckoning
The Shire Reckoning was a version of Kings' Reckoning adapted to fit hobbit customs. Initially, it was identical to Kings' Reckoning but with the days and months named for Northern Mannish terms, which are not provided in their original forms, only in Anglicised versions. Afteryule (Frery), Solmath (Somath), Rethe, Astron (Chithing), Thrimidge, Forelithe (Lithe), Afterlithe (Mede), Wedmath, Halimath (Harvestmath), Winterfilth (Wintring), Blotmath (Blooting) and Foreyule (Yulemath) were the months, with the first and last days of the year being 2 Yule and 1 Yule respectively, and the middle days being 1 Lithe, Mid-Year's Day and 2 Lithe. The leap day was termed Overlithe. The weekdays around the end of the Third Age were Sterday, Sunday, Monday, Trewesday, Hevensday, Mersday and Highday. During the time of Isengrim II (SR.1083-1122, III.2683-2722) it was decided that Mid-Year's Day and the Overlithe would no longer be part of the weekday cycle, causing the year to always start on a "Saturday".
It is believed that hobbits reckoned days from midnight to midnight (S-R). This contrasts with the elves' sunset to sunset and the Númenoreans' sunrise to sunrise.
The year count in the Shire was also unique, dating from the founding of the Shire in III.1601 which was designated SR.1. In Bree the first year was instead III.1300, the year of the founding of Bree. It is not known if Shire Reckoning adopted the full intercalation scheme of Kings' Reckoning, but it is known that century years were indeed skipped (based on the Shire's count). It is probable that the calendar was synchronised with Stewards' Reckoning by the end of the Third Age (how this would have occurred is unknown), but Tolkien's "translation" of the month names when he describes the New Reckoning (is "22 September" in Shire or Stewards'?) makes this ambiguous. In the below analysis I will assume that the two were synchronised throughout the last century of the Third Age.
(The first edition stated explicitly that the corrections had filtered through to the rest of the west of Middle-earth by the War of the Ring.)
Interesting piece of trivia: The Shire Reckoning has been proposed for serious adoption at least once, according to Kristine Larsen. I can't read the article in question because my access only goes back to 1998; if anyone has a copy please let me know.
1d: Stewards' Reckoning
It was inevitable that Kings' Reckoning would drift against the solar year when used over the course of many millennia.(*1) This was exacerbated when it was decided that the year after II.3441 would be the first year of the Third Age and the calendar would use this new numbering, effectively shifting the leap year cycle and introducing a further deficit. Shortly after Mardil became the first Ruling Steward he declared a special addition of 2 days to III.2059, and implemented a new calendar to take effect in III.2060. The new calendar reduced months 6 and 7 to 30 days and added two more days outside the months, tuilerë (spring-day) between months 3 and 4, and yavierë (autumn-day) between months 9 and 10. (The first edition stated that the two days were added to III.2060 instead of III.2059).The calendar was adjusted once more in III.2360 which had an extra day introduced by Hador making it a double-leap year. The Númenorean intercalation system was supposed to continue, but a note further in TC implies that the adjustment in III.3000 was skipped (making it a common year), leaving the calendar once again in deficit, at least according to Tolkien's calculations.
Between its introduction and the War of the Ring the Stewards' Reckoning was adopted by most users of the Westron language, the notable exceptions being residents of the Shire and Bree, who continued using the Shire Reckoning.
(*1) I add here that even our longest-lasting calendars have survived no more than 2000 years or so before being revised or dropping out of use.
1e: New Reckoning
The New Reckoning was implemented shortly after the War of the Ring (exactly when is unclear). Its key feature was that its yestarë fell on 25 Súlìmë in the previous calendar (25 Rethe Shire-reckoning), the date of the destruction of the Ring. Tolkien wrote that it "represented a return to Kings' Reckoning, adapted to fit a spring beginning as in the Eldarin loa", however many (e.g. Möhn) have observed that it has more in common with Shire-reckoning. The months were the same though shifted back by five days or so. There were five days outside the months, yestarë and mettarë were at the start and end of the year as usual (presumably - the text only implies this), but between Yavannië and Narquelië there were three enderi, the middle of which was loëndë. In addition, 30 Yavannië (22 Halimath Shire, 23 Yavannië Stewards') was known as Cormarë (ring day) and the leap day was a doubling of this feast, thus preceding the first enderë. It is unknown whether the New Reckoning inherited the Númenorean leap scheme.
New Reckoning replaced Stewards' Reckoning over the course of King Elessar's reign so that by IV.120 the former was in sole use throughout his lands. Shire Reckoning continued, however.
Due to the change in the start of the year, there is some confusion when converting between Fourth Age years and Third Age years. The most correct way to do so (for the Gondorian reckoning) is by taking the (presumably "old-style" proleptic Stewards' Reckoning) Third Age year, then subtracting 3021 if the date fell before 25 Súlìmë and 3020 if on or after. This is equivalent to taking the Shire Reckoning year and subtracting 1420 or 1421 as required. For example, the death of Aragorn Elessar in III.3141 (Appendix A) or SR.1541 (Appendix B) fell on 1 Rethe and thus falls in IV.120 (subtract 1421); conversely, since Findegil's copy of the Red Book was completed in SR.1592 and IV.172 (subtract 1420) it would follow that it must have happened on or after 25 Rethe. Subtracting 1420/3020 without checking the date of the year, as done by The Thain's Book for Gondorian dates, is not strictly correct.
This is not the only source of confusion when converting dates. In particular, as pointed out in the above Thain's Book link and this thread on the Barrowdowns forum among other places, hobbits appear to have used a different convention; while Gondor considered IV.1 to begin on 25 Súlìmë III.3021 (proleptic Stewards' Reckoning), the Shire considered the Fourth Age to begin on 2 Yule SR.1422, or the first year after the departure of the Three Rings, instead of before. Indeed, both systems can be demonstrated in the text: Éomer's death is given as III.3084 or IV.63 in Appendix A, while Peregrin retired to Gondor later that same year (SR.1484) in the Shire Reckoning, but in IV.64 in the New Reckoning (Prologue), yet according to Appendix B Éomer's death occurred in the autumn, forcing both dates to be in the same year in both Shire and New Reckoning. Assuming the entirety of Appendix A (excluding quotes) was compiled by hobbits, this seems to be a reasonable theory (the two dates in the Prologue are attributed to a scribe in Gondor); however, since the source was moved to Minas Tirith in SR.1484 we cannot be truly sure.
However, the Shire calendar never actually used the Fourth Age reckoning, so strictly speaking only the first method should be used. Thus, in this text all Third Age dates are Stewards' Reckoning (proleptic where necessary) and all Fourth Age dates are New Reckoning so that the previous paragraph applies (not that it becomes relevant to the analysis).
I finally note that the discrepancy is also recognised by the Encyclopedia of Arda, which suggests that the second system above was an "informal" system (as opposed to explicitly attributing it to hobbits like the other sources referenced).
1f: The calendars in The Peoples of Middle-earth
This section will briefly cover the structures of the calendars described in the twelfth part of The History of Middle-earth (nomenclature is mostly omitted). This is divided into multiple manuscripts, of which D1 and D2 are past revisions of Appendix D, while a separate text describes the calendar of the New Era. Although this is not relevant to the below analysis, I note that such descriptions are vague at best in online sources and thus have decided to provide them for completeness.
In both D1 and D2 the Eldarin calendar had a base year of 366 days or 61 full weeks, divided into six 31-day months (1,3,5,8,10,12) and six 30-day months (2,4,6,7,9,11), with occasional short years of 360 days divided into 12 30-day months, usually at the end of an 8-year cycle.(*2) Both versions have a mean year of 365.24 days exactly (as do all the other calendars in these manuscripts), but this was achieved in different ways in each version. In D1, one day was subtracted from the last month of a common year each century (the position of such a year is not stated) and its weekday skipped, giving the calendar a 200-year cycle with 360-day years once in every 8. In D2, the last cycle of a century (quantien) was truncated to 4 years, so that there were 13 short years in every century. The two days to be re-added were placed at the beginning and end of the century, with no weekday name or month. The start of the year is not stated in D1, but in D2 centuries in the elven calendar were intended to begin as closely as possible to the winter solstice.
The Shire Reckoning in both manuscripts is identical to the published version, but is always stated to be derived from Kings' Reckoning, which is different in each version. D1's version of the Kings' Reckoning had twelve 30-day months, with five "Summerdays" between the sixth and seventh, the middle day being doubled in leap years (every fourth year except the last of a century). D2's version had one Midyear's day outside the months (doubled in leap years) and four long months, being the 1st, 6th, 7th and 12th. D2 also introduces the Stewards' Reckoning for the first time; this turns out to be the same as D1's Kings' Reckoning.
The calendar of the New Era began on 25 Rethe (stated to be the 25th in Shire, Kings' and elven reckonings and 26th in D2's Stewards' Reckoning), and had 12 30-day months which were grouped into 5 seasons: Spring (2 months), Summer (3 months), Autumn (2 months), Winter (3 months) and Stirring (2 months). There were two extra days at the start (Spring-days), one in the middle (Mid-year's day, two in leap years) and two at the end (Stirring-days). The middle had no weekday name, following the Shire practice. Dates were officially stated based on seasons (an example can be seen in the King's Letter from the Epilogue in Sauron Defeated, which is quoted by Möhn - also implying that NR.1 began in SR.1420), but the months were also used.
(*2) As an aside, the closest real-life calendar to this arrangement was that used by the Taiping Heavenly Kingdom from 1853-1864, which also had a base year of 366 days, and would have been corrected every 40th year by reducing all months to 28 days, giving a mean year of 365.25 days. It is doubtful that Tolkien was aware of this, given that the calendar has always been extremely obscure.
Part 2: A breakdown of the rest of Tolkien's analysis
This part is dedicated to analysing in detail the rest of his writing in TC, and filling in some of the thought processes behind his statements.
2a: Reconstructing Tolkien's calculations of calendar drifts
Tolkien begins by assuming a fixed year length of 365 days 5 hours 48 minutes 46 seconds. From this, the average drift over a 4-year period is equal to (5h48m46s)*4 - 1 day = -44 minutes 56 seconds (note that this drift is defined as instant of mean event less instant of day start, so a positive drift corresponds to the event occurring after the original date). Over 100 years this becomes (-44m56s)*25 + 1 day = +5 hours 16 minutes 40 seconds. Multiplying this by ten gives an unadjusted drift of +2 days 4 hours 46 minutes 40 seconds. Thus, appending two days in each millennial year gives a drift of +4 hours 46 minutes 40 seconds, as given by Tolkien.
Moving on to the implicit drifts over the Second Age and first two
millennia of the Third Age, assuming the above fixed year length:
II.1: 0 (by definition)
II.1001: +04:46:40
II.2001: +09:33:20
II.3001: +14:20:00
II.3401: +1d11:26:40 (+21:06:40)
II.3441: +1d03:57:20 (-07:29:20)
III.1: +1d09:46:06 (+05:48:46)
III.1001: +1d14:32:46
III.2001: +1d19:19:26
III.2057: +1d08:50:22 (-10:29:04)
At this point it may be instructive to begin by considering the drifts Tolkien would have calculated had the Kings' Reckoning continued through III.3021.
III.2061: +1d08:05:26
III.2101: +2d00:36:06
III.2301: +2d11:09:26
III.2357: +2d00:40:22
III.2361: +1d23:55:26
III.2401: +2d16:26:06
III.2901: +3d18:49:26
III.2941: +3d11:20:06
III.3001: +2d00:06:06
III.3021: +1d20:21:26
Zooming in on particular periods:
III.2058: +1d14:39:08
III.2059: +1d20:27:54
III.2060: +2d02:16:40 --> +1d02:16:40
III.2358: +2d06:29:08
III.2359: +2d12:17:54
III.2360: +2d18:06:40 --> +1d18:06:40
III.3017: +1d21:06:22
III.3018: +2d02:55:08
III.3019: +2d08:43:54
III.3020: +2d14:32:40 --> +1d14:32:40
From here, we begin to look at what Tolkien specifically said. Regarding the period near III.2060, he stated that 2 days were added to III.2059, a new calendar was implemented in III.2060, and after the adjustments the drift was around +8 hours. Regarding the period near III.2360 he only stated that the pre-adjustment drift was less than +1 day (and presumably more than +0). Regarding the period near III.3020, he stated that at "the end of the Third Age" the drift was less than +1 day, which also implied that it was more than +0 also. Because of this we begin by concluding that the net adjustment by III.3021 was 1 day, making the drift 20:21:26. Where we run into trouble is when including the corrections in III.2059 and III.2360. The 8 hours clearly refers to III.2061, implying that 1 day was appended by then, but we know two days were added. What is unclear is whether his other statement includes or excludes the leap day of III.2360 that already existed. If it includes the leap day (thus corresponding to a smaller value such as 1d18:06:40), then the one extra day must fall between III.2361 and III.3021. However, Tolkien states that no further adjustments were made, so the only place for such an error would be III.3000. In this case, III.3000 would be a regular leap year, which has never occurred on a century year before; such an event would likely have been commented on. If the III.2360 statement excludes the leap day (then 2d18:16:40 less two days), then the error must be in the calculation for III.2061, and the drift then would be -15:54:34. In my opinion, the most likely explanation for the discrepancy here is that Tolkien stepped forwards from the III.2050s in his calculations and forgot that III.2060 was leap, which corresponds to the second case. This will be assumed for the rest of the analysis.
As an aside, Möhn has his own construction in which he concludes that the leap day in III.2060 was omitted and his calculations seemingly support this. They are also wrong - his 0.4 days (9.6 hours) and 0.77 days (18.5 hours) cannot be matched with any of the figures above. What seems to have happened is that he made a sign error in computing the III.2061 drift and ended with -8 hours instead of +8. By contrast, the figures above agree with the calculations of Ake Jonsson, in Beyond Bree ("The Kings' Reckoning: Did Tolkien Reckon Correct?" November 1985, quoted in the Reader's Companion), once one applies the assumption that the leap day in III.2060 was omitted (Jonsson was unable to match the III.3021 drift). Unfortunately, I don't have access to a copy of this article, so I can't verify the above at the moment.
I note by the way that Möhn moved his website in c.2007 and no-one noticed until 2014, least of all the Internet Archive. Infuriatingly, most of his essays are now in paid book (print and digital) form, including ones that don't appear to have any archived counterpart. While I would have no problem finding 4 euros to pay for the ebook, I do have a goal of compiling this entire article solely from freely available sources, so material from the paid book will not be incorporated in the foreseeable future.
2b. Why we know the Calendar of Imladris has no further adjustments
The Calendar of Imladris does not have a known epoch. Despite this it is still possible to analyse its relation to the other reckonings with a little care. The only correlation is given for III.3019, but we can subtract multiples of 432 due to the known cycle length. Thus, going back 6048 years gives us II.412. In that period the Rivendell calendar intercalated 35*14=490 times, while in the Kings' and Stewards' reckonings there were 22+24*4+26+242*2+24*4+10+242*3+1+4=1465 leap days. Thus, yestarë of Rivendell in that year fell 5 days earlier than in III.3019, or on 1 Víressë (Kings' Reckoning).
To return to II.1, we need to subtract 411 years. In such a period there are 35 full cycles and 3 years remainder, so there were either 34, 35 or 36 intercalations. In Kings' Reckoning there were 24*4+2=98 leap days, so yestarë would have fallen either on 27 Súlìmë, 24 Súlìmë or 21 Súlìmë. On the other hand, 35 and 36 are extremely unlikely (requiring the start of a cycle in the last 21 years of the First Age) so most likely it would have fallen on the 27th.
What if we assume an epoch for the calendar, say I(s).1? Then the first leap year after II.1 would be II.10, the next skipped would be II.274 and there are 34 intercalations between II.1 and II.412. Between II.1 and II.12 yestarë would fall on 27, 27, 27, 27, 26, 26, 26, 26, 25, 25, 28, 28 Súlìmë; in II.275, the first year of a cycle, yestarë would fall on 30 Súlìmë. This is certainly closer to where one would expect the elves would begin their year, especially if they wanted to put it close to the spring equinox - or for that matter, put the enderi close to the autumn equinox.
2c: What did Thursday 21st of April actually mean?
Or, rather, "the 21st of April, a hundred years ago last Thursday". (I seem to remember that some edition read Friday instead, but I checked recent editions and even the 2014 movie tie-in versions are based on the 1995 and read Thursday.) So, let's go over the possibilities, keeping in mind that Gandalf and Thorin would likely use the Stewards' Reckoning as their primary calendar:
- It was an error, and Tolkien meant Friday/Highday. This is the most obvious option, and the easiest way to correct the scene without contradictions.
- It was an error, and Tolkien meant the 20th. This is the second most obvious option, but considerably less plausible. By the way, I don't believe Bilbo would have let such an obvious error (to him) slip by, so these first two cases would have to be attributed to errors in Tolkien's purported translation.
- It was actually a Stewards' Reckoning date. 21 Víressë corresponds to 22 Astron in Shire-reckoning, so we can deduce the weekday sequence from there. Bilbo would be confused though, as would Tolkien.
- It was a Shire date with a Stewards' weekday. Mixing calendars is dangerous, but at least we can deduce the Stewards' date in this as well (20 Víressë), and also the weekday sequence.
- It was a Stewards' date with a Shire weekday. More calendar-mixing. However, since the corresponding Shire date should be the 22nd, which was a Sterday/Saturday, this implies that the Shire and Stewards' Reckonings are out by two days. This might have been explained by all the calendar changes in the Stewards' Reckoning, except that it is known that the calendars were synchronised by the War of the Ring. Of course, it's possible the correction only went through after the events of the Hobbit.
Combining this with sources (e.g. the Quest for Erebor) that state that the Unexpected Party took place on "Wednesday" (i.e. Hevensday) 26 Astron, it's probably best to stick to option 1 and not complicate things.
And for those of you who are tempted to claim that the Shire Reckoning hadn't been invented yet, the current wording was used as part of Tolkien's timeline calculations for the aborted 1960 Hobbit. Moreover, until the second edition of 1951 the line in question read "the 3rd of March, a hundred years ago last Thursday". Be thankful that egregious error was fixed.
Part 3: What errors did Tolkien actually make? - moon phase errors
It is well known that Tolkien was quite pedantic about the passage of time in the narrative, even rewriting a section that had inconsistent moon phases. It is slightly less well known that he decided to do so by taking the new and full moons of 1941/2 and shifting them a few days, as demonstrated by the manuscript quoted in the Reader's Companion. Despite this, as pointed out by S-R, he still managed to screw up.
In particular, the period between the new moon of 22 Solmath and the full moon of 8 Rethe is impossible since it would require at least 16 full days but no such period takes more than 15 days 15 hours, at least in the modern era (Bromberg); this error is attributed to Tolkien confusing the new crescent moon with the astronomical new moon (dark moon), which is not visible. However, we know that LotR takes place some millennia in the past, so what can we say about how this affects the analysis? Estimating from Bromberg's graphs suggest that the extra error in -7000 was only 0.02 day in each direction, for a total of about 1 hour. In fact, having run the numbers myself, the longest period between new and full moons between -15000 and 2000 equals 15 days 16 hours 8 minutes, to the nearest minute (it's in July of 14634 BCE in the proleptic Julian calendar, in case you're wondering). This is clearly not enough to resolve this issue. S-R also supplies three other examples of errors during the events:
- During Frodo's dream of Gandalf while staying at the house of Tom Bombadil, where he sees a "young moon rising" despite the fact that this is impossible. This is attributed to dream confusion; later accounts are vague on the nature of the moon.
- The West Gate of Moria, where a waning gibbous moon shines on a presumably westward-facing cliff early in the night; again impossible since the waning moon passes its zenith after midnight. This is a relic of earlier versions of the text, where the moon was actually waxing at that point, and was not removed along with the other references when the revision was made. Hammond and Scull considered revising this for the 2004 edition, but eventually decided that the reference was crucial to Tolkien's vision of the scene, so the error remains in the most recent edition.
- The third is two days after that, where what should be a last quarter moon is described as "sickle". This is only slightly off.
There is one last error, this time at the end of the narrative - the "Moon went westward" when the moon should have been new.
For our next error, we turn to The Hobbit. Now it is well known that The Hobbit was written first and intended to be stand-alone, so errors that relate between this and Lord of the Rings can be somewhat forgiven. Both Strom and Möhn have observed that assuming the modern-day value of the mean synodic month would imply that the moon phases in The Hobbit and The Lord of the Rings were inconsistent, with the former stating explicitly that the midsummer's eve crescent moon in the evening (and thus waxing) should have been a waning gibbous if that were the case. Calculating back from 8 Rethe SR.1419 places the nearest full moon to Mid-Year's Day SR.1341 about 28379 days earlier, on the night of 27 Forelithe, which makes the moon on the night of 1 Lithe about 19 days old, almost exactly half a lunar cycle from the intended phase. This also implies that Durin's Day falls around 7 Blotmath as opposed to 22 Winterfilth which is given by Möhn or Strom’s 20 Winterfilth - not that we have a proper definition for the dwarves' autumn anyway. Still, this cannot be resolved so easily; the moon is mentioned many other times in The Hobbit. Refer to Möhn for a full list and Part 7 for my attempt at a chronology.
And of course we can't discuss moon phase errors without mentioning the most egregious of all: A rising waxing moon on the day after Durin's Day? Clearly impossible, since a waxing moon rises during the daytime. This is the most blatant error in the entire legendarium.
Part 4: What errors did Tolkien actually make? - Year length errors
By now you may have guessed from all the carefully placed qualifiers in Part 2 that this is the critical point that motivated this analysis.(*3) In short, Tolkien's year length is only valid for a few hundred years near the year 1900, and once one allows for the changing year length the entire meticulously thought out scheme collapses.
Firstly, what kind of year is Tolkien referring to? The value he gives is that of the mean tropical year as defined in modern times, in other words the average amount of time required for the Sun's longitude to increase by 360 degrees (for example, northern equinox to northern equinox, or southern solstice to southern solstice). However, if we fix a point in the year (e.g. southern solstice) and measure the year length, due to the eccentricity of the Earth's orbit this will not be the same as the mean tropical year. This is also closely associated with variation in the lengths of the seasons; all the reasons for this are explained quite succinctly on Bromberg's page. We will see the impact of this in more detail in part 5.
The change in the length of the mean tropical year in terms of solar days over time can be broken down into changes in the Earth's orbit and changes in the length of the solar day.
We first introduce the concept of DeltaT (ΔT), the time difference between Terrestrial Time and Universal Time (specifically, UT1). Terrestrial Time is defined using a base unit of atomic seconds, while UT1 is defined using mean solar days. (UTC is a hybrid, ticking atomic seconds but with manual adjustments at irregular intervals - leap seconds - to match UT1.) The Earth's rotation is not constant, owing mainly to tidal forces. Due to this, the length of the day is slowly increasing over time.
Thus, to determine the impact of the change of Earth's rotation on the length of the year, we can find the equation for the change in DeltaT over the course of a year based on a given DeltaT approximation. For example, the approximation for distant time periods used by Espenak and Meeus (2005) is -20+32t^2, where t is Julian centuries from 1820. The first derivative multiplied by 0.01 (= 0.64t) gives the change over one year. Setting t = -58.8 gives the approximate lengthening in -4000 (the rough era of the War of the Ring, according to a footnote in Letter 211) as 37.6 seconds. Alternatively, one can assume a fixed rate of change of the length of day and calculate from there; Monteiro assumes 1.6ms/century which gives around 35 seconds, while Bromberg's 1.75ms/century gives 38.35 seconds.
We have concluded that owing to the slowing of the Earth's rotation the length of the year 6000 years ago would have been over a half-minute longer than at present. However, what if we ignored this and used fixed-length days? This leads us to consider the second component of the change of the year, namely that caused by changes in the Earth's orbit, and the component that seems to have been missed by all previous analyses, even the ones which took into account the changing day length such as Monteiro (although the formula used by Belyakov incorporates both components, he does not mention changes in the orbit).
For this, we turn to Bromberg (again), who informs us that the Earth's obliquity cycle causes its orbital period to vary quasi-periodically over the span of 41000 years. Reading off his graphs we find that in -4000 the year length in atomic days was roughly 365 days 5 hours 49 minutes 12 seconds - exactly the mean year length of the Gregorian calendar. Alternatively, setting T=-60 in Lasker's expression for the mean tropical year gives 365.2424992 days, which rounds to the above. Thus, the orbital component of the change in the length of the solar year comes to some 26 seconds at the time of the War of the Ring.
At any rate we can't ignore the change in the length of the day, since for calendar drift purposes we must consider calendar days, which are mean solar days, not to mention the fact that when TC was published in 1954 the second had not yet been defined as a fixed length (this would only occur two years later).
At this point you may be wondering, "What if these factors weren't known in Tolkien's time?" To this I point out that LeVerrier recognised that the length of the tropical year was changing in the 19th century, as did Simon Newcomb in his tables of 1898 (which were used as the standard for the Astronomical Almanac until the 1980s), while the Earth's slowing rotation was identified in 1864 by Ferrel and calculated as early as 1927 with de Sitter's work. Whether Tolkien would have discovered this had he put a significant amount of effort into researching this, we cannot be sure; suffice to say that it is clear that he was not aware at all.
In conclusion, the two factors combine to result in a change of some 65 seconds in the length of the mean tropical year in the past 6000 years. So much for "the year was no doubt the same length".
By the way, Bromberg has a handy graph that summarises the lot. Several, in fact.
(*3) In the course of researching this article I discovered that this had been pointed out as far back as 1995, in a thread buried on Usenet, but the analysis there was not nearly as comprehensive as that done here.
Part 5: What are the implications of the above "errors" and how do they impact existing analyses?
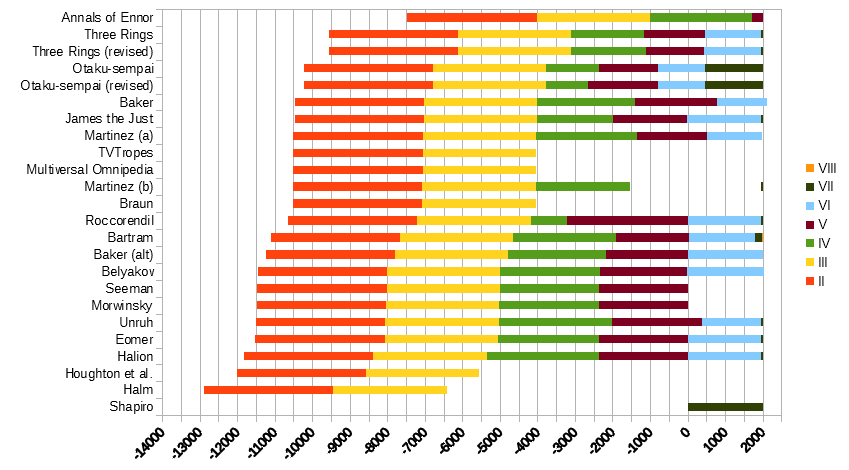
In the past many have attempted to fix the date of the start of the Fourth Age and/or subsequent ages against the Common Era year numbering system. As one may expect, these span a wide range between them, as displayed in the following table (reverse chronological order of Fourth Age):
| Eighth Age | Seventh Age | Sixth Age | Fifth Age | Fourth Age | Third Age | Second Age | ||
|---|---|---|---|---|---|---|---|---|
| 2004(-) | Annals of Ennor | |
n/a | n/a | 1713 | ~-1000 | ~-4021 | ~-7462 |
| 2004, 2013 | Three Rings (original) | n/a | 1954 | 454 | -1171 | -3101-03-19 | -6122-12-24 | -9563-12-26 |
| 2013 | Three Rings (revised) | n/a | 1954 | 445 | -1102 | -3101-03-19 | -6122-12-24 | -9563-12-26 |
| 2014 | Otaku-sempai | n/a | 476 | -799 | -2348 (later -2649) | -3758 | -6779 | -10220 |
| 1998 | Baker | n/a | 2120 or 2001 | 780 | -1399 | -3999 | -7020 | -10461 |
| 2011 | Strom | n/a | 1945 | -5 | -1999 | -4005-03-16 | -7026-12-21 | -10467-12-24 |
| 2012 | TVTropes | |
|
|
|
-4039 | -7060 | -10501 |
| 2004 | Martinez (a) | |
|
550 | -1318 | -4039 | -7060 | -10501 |
| 2004(-) | Multiversal Omnipedia | |
|
|
|
-4040 | -7061 | -10502 |
| 2013 | Martinez (b) | |
1945 | ??? | -1541 | -4041 | -7062 | -10503 |
| 2001? | Braun | |
|
|
|
-4041 | -7062 | -10503 |
| 201x | Roccorendil | n/a |
1945 | 0 | -3200 | -4179 | -7200 | -10641 |
| 2015 | Bartram | 1992-02-28 | 1789 | 33 | -1920 | -4640 | -7661 | -11102 |
| 1996 | Baker (alt) | n/a | 2000 | 1 | -2179 | -4779 | -7800 | -11241 |
| 2004 | Belyakov | n/a | 2040 | -4 | -2333 | -4985 | -8006 | -11447 |
| 1999 | Seeman | |
|
~0 | -2347 | ~-5000 | ~-8021 | ~-11462 |
| 2010 | Morwinsky | |
|
~0 | -2347 | -5018 | -8039 | -11480 |
| 2006 | Unruh | n/a | 1945 | 395 | -2017 | -5033 | -8054 | -11495 |
| |
|
|
|
|
~-200000000 | |
|
|
| 2002 | Eomer fix link | n/a | 1945 | 0 | -2348 | -5053 | -8074 | -11515 |
| 2002 | Halion (reconstructed) | n/a | 1945 | 0 | -2348 | ~-5348 | ~-8369 | ~-11810 |
| 1972 | Houghton et al. | |
|
|
|
-5551 | -8572 | -12013 |
| 2000 | Shapiro | n/a | 1 | |
|
|
|
|
| 2004(-) | Halm | |
|
|
|
-6416 | -9437 | -12878 |
| 2014(-) | Mangum | |
|
|
-25037 | -28058 | -31499 | |
| 2008(-) | ??? | |
|
|
-33199 | -38609 | -41630 | -45071 |
| 1967 | Howes (Tolkien Journal #8) | -86588 | -89609 | -93050 |
Note that owing to uncertainty in the length of the First Age (both due to uncertainty in the length of the Valian Year - though the figure of 84000 hours is generally accepted - and uncertainty in the time elapsed between the first rising of the Sun and the end of the Age) it has been omitted. Joseph Bongiorno's proposal has also been omitted due to the significant inconsistencies in the dates provided.
Here is a graphical comparison of the various datings (excluding the two outliers). The periods have been extended to 2016 where necessary. Note the two clumps around -4000 and -5000.
Tolkien himself claimed in letter 211 (dated 1958-10-14) that the Fourth Age would have started around 6000 years ago (more than one of the dates above were found by subtracting 6000 years from the writing of this letter) and that we are likely near the end of the Sixth or the start of the Seventh Age. He would also make a remark in 1971 about not being able to work out lunar and solar positions 7000-8000 years ago (as mentioned by Seeman and quoted in full in HoME). With this in mind, we discard the dates before -6000 and after -2000. Indeed, by considering the effects of precession (as done by Monteiro, as well as James Strom in this recent article published in Beyond Bree) one can see that if the Fourth Age had not started near -4000 it would need to have begun in the vicinity of -11000 or earlier.
Furthermore, all except three of the dates given here have no astronomical analysis to back them up (the -5551 date is explicitly PFA), and of those three only two have provided exact days, and so we put aside all except the -3101 and -4005 dates for now.
We will go through the two main analyses in detail. First is the analysis by Tony Steele (a.k.a. Ash Branch), henceforth referred to as the Three Rings, or 3R analysis (after the website on which it is published), published in the 2004 issue of Mallorn, which through matching the 6462 years between the sinking of Atlantis and the start of the Fourth Age (i.e. the Kali Yuga, see Wikipedia for more details) in Theosophical doctrine with the corresponding period between the sinking of Beleriand and the start of the Fourth Age of Middle-earth places the first day of the Second Age at -9563-12-26 Gregorian (9563 BCE/03/10 Julian, JDN -1771394) and the tenth day of III.3019 at -3104-12-31 Gregorian (3104 BCE/01/26 Julian, JDN 587713). As a result, the Fourth Age begins in -3101, with 2 Yule SR.1421 corresponding to -3102-12-22, 25 Rethe corresponding to -3101-03-17, and 22 Halimath to -3101-09-14. The original version of the article made no mention of subsequent ages, with conjectures of further ages being added in 2013 and revised later that year.
This analysis already has problems, most notably the fact that it is based on the Annals of Beleriand (the sinking of Beleriand occurring in I(s).597, or the last year of the First Age), whereas in the Grey Annals the corresponding period is 6465 years (I(s).587 to III.3021); although the figures in the later sections of the analysis were subsequently updated in 2013 with the more recent figure (the pre-update version can be found on the Internet Archive) this one cannot be owing to its underpinning the entire analysis. Any attempt to explain the discrepancy here will move into very speculative territory; in particular, Bartram has thoroughly criticised the claims Steele made, pointing out that the two dates come from completely unrelated parts of the system, to which he also adds that Steele's contention of Tolkien being involved in Theosophy is itself suspect, with no evidence provided apart from the aforementioned link which by this point starts to look rather forced. Also, Steele gives far too much credit to Tolkien's astronomical knowledge (see parts 3 and 4). Finally, his calculated full moon is roughly 16 hours late, at least according to the program SOLEX which puts the moon in question at 17:07:51 on -3104-12-30.(*4) Thankfully, the error is mitigated since he assigned the 31st to the later day instead of the earlier possibility.
The second analysis, by James Strom, also known as James the Just (thus henceforth the JtJ analysis) and dating from 2011, starts by taking as a first estimate Tolkien's 6000 years before 1958 (giving -4042), then eliminates years from the 500 years each side of that date based on moon phase analysis, and finally based on the brightness and position of Venus in the sky during the Mirror of Galadriel scene on 14 Solmath (*5) which he correlates to -4007-02-02 (4008 BCE/03/06 Julian). It should be noted that his bounds for the ninth day of III.3019 were between 26 and 29 December (PGC), which does not include the 30 December implied in the 3R analysis. His date for the first day of the Second Age is -10467-12-24 (10467 BCE/03/14 Julian) and for the tenth day of III.3019 -4008-12-30 (4008 BCE/01/29 Julian). His Fourth Age begins in -4005; 2 Yule SR.1421 corresponds to -4006-12-21, 25 Rethe to -4005-03-16 and 22 Halimath to -4005-09-13. Incidentally, he also uses the 597-year length from the Annals of Beleriand when he calculates the start of the First Age, but this is not relevant to the rest of his analysis.
At this point, we may consider the sky over Lorien at the time of the Mirror of Galadriel scene (3R: -3103-02-05 or 3104 BCE/03/04; JtJ: -4007-02-02 or 4008 BCE/03/06), one hour after sunset. A quick check of the 3R date finds that Venus is on the wrong side of the sun; conversely the JtJ date shows Venus near peak brightness and observing angle. While we're at it, if we check the other explicit years for around 3 February (proleptic Gregorian), -3760 is also on the wrong side of the sun, as are -4043 and -5055; -4001 and -4041 are at least on the correct side of the sun, but are not especially bright; -5553 is surprisingly suitable (giving very similar results to -4007) and -6418 is somewhere in between.
Let us now list the dates of the corresponding solstices for the two above datings, in TT and UT. Standard error is <1 minute for TT and large for UT. All such times are computed using SOLEX version 11. When reading the below table, remember that dates before III.2059 are Kings' Reckoning and from III.2060 onwards are Stewards' Reckoning, so the last day of Náríë is the 31st before III.2060 and the 30th after III.2060.
| Solstice | 3R year | JD | TT | UT | KR/St.R date | JtJ year | JD | TT | UT | KR/St.R date |
|---|---|---|---|---|---|---|---|---|---|---|
| II.0/1 Winter | -9563/2 | -1771398.846 | 9563 BC/03/05 15:42 | 9563 BC/02/28 20:33 | II.0 Ringare 22 | -10467/6 | -2101577.508 | 10467 BC/03/12 23:49 | 10467 BC/03/07 09:39 | II.0 Ringare 25 |
| II.1 Summer | -9562 | -1771216.262 | 9563 BC/09/04 05:42 | 9563 BC/08/30 10:34 | II.1 Narie 23 | -10466 | -2101396.090 | 10467 BC/09/10 09:50 | 10467 BC/09/04 19:41 | II.1 Narie 24 |
| II.1000/1 Winter | -8563/2 | -1406156.930 | 8563 BC/02/25 13:41 | 8563 BC/02/21 13:53 | II.1000 Ringare 23 | -9467/6 | -1736335.617 | 9467 BC/03/04 21:11 | 9467 BC/02/28 03:58 | II.1000 Ringare 26 |
| II.1001 Summer | -8562 | -1405973.062 | 8563 BC/08/28 10:31 | 8563 BC/08/24 10:43 | II.1001 Narie 25 | -9466 | -1736152.910 | 9467 BC/09/03 14:10 | 9467 BC/08/29 20:57 | II.1001 Narie 26 |
| II.3318/9 Winter | -6245/4 | -559525.838 | 6245 BC/02/07 15:52 | 6245 BC/02/05 06:05 | II.3318 Ringare 28 | -7149/8 | -889704.742 | 7149 BC/02/14 18:11 | 7149 BC/02/11 18:42 | II.3318 Ringare 30 |
| II.3319 Summer | -6244 | -559339.598 | 6245 BC/08/11 21:38 | 6245 BC/08/09 11:51 | II.3319 Narie 30 | -7148 | -889519.273 | 7149 BC/08/18 05:27 | 7149 BC/08/15 05:58 | II.3319 Loëndë |
| II.3440/1 Winter | -6123/2 | -514966.303 | 6123 BC/02/06 04:43 | 6123 BC/02/03 20:40 | II.3440 Ringare 26 | -7027/6 | -845145.198 | 7027 BC/02/13 07:14 | 7027 BC/02/10 09:41 | II.3440 Ringare 28 |
| II.3441 Summer | -6122 | -514779.975 | 6123 BC/08/11 12:35 | 6123 BC/08/09 04:32 | II.3441 Narie 31 | -7026 | -844959.610 | 7027 BC/08/17 21:22 | 7027 BC/08/14 23:49 | II.3441 Loëndë |
| II.3441/2 Winter | -6122/1 | -514601.055 | 6122 BC/02/06 10:40 | 6122 BC/02/04 02:38 | II.3441 Ringare 27 | -7026/5 | -844779.950 | 7026 BC/02/13 13:11 | 7026 BC/02/10 15:39 | II.3441 Ringare 28 |
| III.1 Summer | -6121 | -514414.728 | 6122 BC/08/11 18:31 | 6122 BC/08/09 10:29 | III.1 Narie 31 | -7025 | -844594.373 | 7026 BC/08/18 03:03 | 7026 BC/08/15 05:31 | III.1 Loëndë |
| III.2058/9 Winter | -4064/3 | 237067.773 | 4064 BC/01/21 06:33 | 4064 BC/01/19 23:48 | III.2058 Ringare 27 | -4968/7 | -93111.435 | 4968 BC/01/28 01:34 | 4968 BC/01/26 08:37 | III.2058 Ringare 30 |
| III.2059 Summer | -4063 | 237254.756 | 4064 BC/07/27 06:08 | 4064 BC/07/25 23:22 | III.2059 Enderi 1 | -4967 | -92924.539 | 4968 BC/08/02 23:04 | 4968 BC/08/01 06:08 | III.2059 Cermie 1 |
| III.2059/60 Winter | -4063/2 | 237433.016 | 4063 BC/01/21 12:23 | 4063 BC/01/20 05:38 | III.2059 Ringare 26 | -4967/6 | -92746.188 | 4967 BC/01/28 07:28 | 4967 BC/01/26 14:33 | III.2059 Ringare 28 |
| III.2060 Summer | -4062 | 237619.996 | 4063 BC/07/27 11:54 | 4063 BC/07/26 05:10 | III.2060 Narie 30 | -4966 | -92559.303 | 4967 BC/08/03 04:43 | 4967 BC/08/01 11:48 | III.2060 Enderi 2 |
| III.2060/1 Winter | -4062/1 | 237798.259 | 4062 BC/01/21 18:12 | 4062 BC/01/20 11:28 | III.2060 Ringare 25 | -4966/5 | -92380.943 | 4966 BC/01/28 13:21 | 4966 BC/01/26 20:26 | III.2060 Ringare 27 |
| III.2061 Summer | -4061 | 237985.235 | 4062 BC/07/27 17:37 | 4062 BC/07/26 10:53 | III.2061 Narie 29 | -4965 | -92194.055 | 4966 BC/08/03 10:41 | 4966 BC/08/01 17:46 | III.2061 Loëndë |
| III.2359/60 Winter | -3763/2 | 347005.785 | 3763 BC/01/19 06:51 | 3763 BC/01/18 03:09 | III.2359 Ringare 27 | -4667/6 | 16826.549 | 4667 BC/01/26 01:10 | 4667 BC/01/24 11:47 | III.2359 Ringare 29 |
| III.2360 Summer | -3762 | 347192.726 | 3763 BC/07/25 05:26 | 3763 BC/07/24 01:45 | III.2360 Enderi 1 | -4666 | 17013.497 | 4667 BC/07/31 23:55 | 4667 BC/07/30 10:32 | III.2360 Enderi 3 |
| III.3018/9 Winter | -3104/3 | 587700.677 | 3104 BC/01/14 04:15 | 3104 BC/01/13 06:42 | III.3018 Ringare 28 | -4008/7 | 257521.351 | 4008 BC/01/20 20:24 | 4008 BC/01/19 14:14 | III.3018 Ringare 30 |
| III.3019 Summer | -3103 | 587887.432 | 3104 BC/07/19 22:21 | 3104 BC/07/19 00:49 | III.3019 Cermie 1 | -4007 | 257708.335 | 4008 BC/07/26 20:02 | 4008 BC/07/25 13:52 | III.3019 Cermie 3 |
| III.3020/1 Winter | -3102/1 | 588431.176 | 3102 BC/01/14 16:13 | 3102 BC/01/13 18:42 | III.3020 Ringare 28 | -4006/5 | 258251.839 | 4006 BC/01/21 08:07 | 4006 BC/01/20 01:58 | III.3020 Ringare 30 |
| III.3021 Summer | -3101 | 588617.917 | 3102 BC/07/20 10:00 | 3102 BC/07/19 12:29 | III.3021 Loëndë | -4005 | 258438.810 | 4006 BC/07/27 07:26 | 4006 BC/07/26 01:17 | III.3021 Cermie 3 |
Here we have a table of selected solstices. Immediately one sees that while things seem to be okay during the late Third Age they go very wrong as one moves back in time to the start of the Second Age. In particular, the dates are falling early for pretty much the entire Second Age, and in the first millennium alone advances over one and a half days.
One also sees that the time between the winter solstice and the subsequent summer solstice increases over the period observed, and reaches a peak of around 187 days in -4000 to -3000. The winter solstice falls early for the entire observed period.
Finally, the JtJ dates can be seen to match the summer solstice more closely in the third millennium of the Third Age compared to the 3R dates. Since two leap days were omitted from III.3000, the solstice falls late in III.3019 in JtJ as expected, but does not in 3R.
But we're not done yet! As one goes further back in the past the uncertainty in the slowing of Earth's rotation is proportional to DeltaT itself, since the factors that affect Earth's rotation are highly variable. What happens if we allow for this margin of error?
| Solstice | UT (Gregorian) | KR/St.R date | s.e. (hms) | -2 s.e. | +2 s.e. | UT (Gregorian) | KR/St.R date | s.e. (hms) | -2 s.e. | +2 s.e. |
|---|---|---|---|---|---|---|---|---|---|---|
| II.0/1 Winter | -9563-12-16 20:33 | II.0 Ringarë 22 | 26:10:13 | Ringarë 20 16:13 | Ringarë 25 00:54 | -10467-12-17 09:39 | II.0 Ringarë 25 | 31:20:25 | Ringarë 22 18:58 | Ringarë 28 00:20 |
| II.1 Summer | -9562-06-17 10:34 | II.1 Náríë 23 | 26:10:03 | Náríë 21 06:14 | Náríë 25 14:54 | -10466-06-16 19:41 | II.1 Náríë 24 | 31:20:14 | Náríë 22 05:01 | Náríë 27 10:22 |
| II.1000/1 Winter | -8563-12-17 13:53 | II.1000 Ringarë 23 | 20:59:21 | Ringarë 21 19:54 | Ringarë 25 07:51 | -9467-12-17 03:58 | II.1000 Ringarë 26 | 25:38:54 | Ringarë 25 00:40 | Ringarë 28 07:16 |
| II.1001 Summer | -8562-06-19 10:43 | II.1001 Náríë 25 | 20:59:12 | Náríë 23 16:45 | Náríë 27 04:42 | -9466-06-17 20:57 | II.1001 Náríë 26 | 25:38:45 | Náríë 24 17:40 | Náríë 28 00:15 |
| II.3318/9 Winter | -6245-12-18 06:05 | II.3318 Ringarë 28 | 11:09:07 | Ringarë 27 07:46 | Ringarë 29 04:23 | -7149-12-17 18:42 | II.3318 Ringarë 30 | 14:37:37 | Ringarë 29 13:26 | Mettarë 23:57 |
| II.3319 Summer | -6244-06-21 11:51 | II.3319 Náríë 30 | 11:09:00 | Náríë 29 13:33 | Náríë 31 10:09 | -7148-06-20 05:58 | II.3319 Loëndë | 14:37:30 | Náríë 31 00:43 | Cermië 1 11:13 |
| II.3440/1 Winter | -6123-12-17 20:40 | II.3440 Ringarë 26 | 10:43:06 | Ringarë 25 23:13 | Ringarë 27 18:06 | -7027-12-17 09:41 | II.3440 Ringarë 28 | 14:07:52 | Ringarë 27 05:25 | Ringarë 29 13:57 |
| II.3441 Summer | -6122-06-22 04:32 | II.3441 Náríë 31 | 10:42:59 | Náríë 30 07:06 | Loëndë 01:58 | -7026-06-20 23:49 | II.3441 Loëndë | 14:07:45 | Náríë 31 19:34 | Cermië 2 04:05 |
| II.3441/2 Winter | -6122-12-18 02:38 | II.3441 Ringarë 27 | 10:42:53 | Ringarë 26 05:12 | Ringarë 28 00:03 | -7026-12-17 15:39 | II.3441 Ringarë 28 | 14:07:37 | Ringarë 27 11:24 | Ringarë 29 19:55 |
| III.1 Summer | -6121-06-22 10:29 | III.1 Náríë 31 | 10:42:47 | Náríë 30 13:03 | Loende 07:54 | -7025-06-21 05:31 | III.1 Loëndë | 14:07:30 | Náríë 31 01:16 | Cermië 1 09:46 |
| III.2058/9 Winter | -4064-12-18 23:48 | III.2058 Ringarë 27 | 04:40:20 | Ringarë 27 14:27 | Ringarë 28 09:08 | -4968-12-18 08:37 | III.2058 Ringarë 30 | 07:01:51 | Ringarë 29 18:34 | Ringarë 30 22:41 |
| III.2059 Summer | -4063-06-23 23:22 | III.2059 Enderi 1 | 04:40:16 | Enderi 1 14:02 | Enderi 2 08:43 | -4967-06-23 06:08 | III.2059 Cermië 1 | 07:01:46 | Enderi 3 16:04 | Cermië 2 20:11 |
| III.2059/60 Winter | -4063-12-19 05:38 | III.2059 Ringarë 26 | 04:40:12 | Ringarë 25 20:18 | Ringarë 26 14:58 | -4967-12-18 14:33 | III.2059 Ringarë 28 | 07:01:41 | Ringarë 28 00:29 | Ringarë 29 04:36 |
| III.2060 Summer | -4062-06-24 05:10 | III.2060 Náríë 30 | 04:40:07 | Náríë 29 19:49 | Náríë 30 14:30 | -4966-06-23 11:48 | III.2060 Enderi 2 | 07:01:35 | Enderi 1 21:45 | Cermië 1 01:51 |
| III.2060/1 Winter | -4062-12-19 11:28 | III.2060 Ringarë 25 | 04:40:03 | Ringarë 25 02:08 | Ringarë 25 20:48 | -4966-12-18 20:26 | III.2060 Ringarë 27 | 07:01:30 | Ringarë 27 06:23 | Ringarë 28 10:29 |
| III.2061 Summer | -4061-06-24 10:53 | III.2061 Náríë 29 | 04:39:59 | Náríë 29 01:33 | Náríë 29 20:13 | -4965-06-23 17:46 | III.2061 Loëndë | 07:01:25 | Loëndë 03:44 | Cermië 1 07:49 |
| III.2359/60 Winter | -3763-12-19 03:09 | III.2359 Ringarë 27 | 03:59:24 | Ringarë 26 19:10 | Ringarë 27 11:08 | -4667-12-18 11:47 | III.2359 Ringarë 29 | 06:11:38 | Ringarë 28 23:24 | Ringarë 30 00:10 |
| III.2360 Summer | -3762-06-24 01:45 | III.2360 Enderi 1 | 03:59:20 | Náríë 30 17:46 | Loëndë 09:43 | -4666-06-23 10:32 | III.2360 Enderi 3 | 06:11:33 | Enderi 2 22:09 | Enderi 3 22:55 |
| III.3018/9 Winter | -3104-12-18 06:42 | III.3018 Ringarë 28 | 02:40:36 | Ringarë 28 01:21 | Ringarë 28 12:04 | -4008-12-18 14:14 | III.3018 Ringarë 30 | 04:32:29 | Ringarë 30 05:09 | Ringarë 30 23:19 |
| III.3019 Summer | -3103-06-23 00:49 | III.3019 Cermië 1 | 02:40:32 | Loëndë 19:28 | Cermië 1 06:10 | -4007-06-23 13:52 | III.3019 Cermië 3 | 04:32:25 | Cermië 3 04:47 | Cermië 3 22:56 |
| III.3020/1 Winter | -3102-12-18 18:42 | III.3020 Ringarë 28 | 02:40:23 | Ringarë 28 13:21 | Ringarë 29 00:03 | -4006-12-19 01:58 | III.3020 Ringarë 30 | 04:32:12 | Ringarë 29 16:54 | Ringarë 30 11:03 |
| III.3021 Summer | -3101-06-23 12:29 | III.3021 Loëndë | 02:40:19 | Loëndë 07:08 | Loëndë 17:50 | -4005-06-24 01:17 | III.3021 Cermië 3 | 04:32:08 | Cermië 2 16:13 | Cermië 3 10:22 |
This table allows for twice the standard error in the value of DeltaT, corresponding to an approximate 95% confidence interval. Even when doing so one can see that the dates still fall several days out from their expected values. This, more than anything else, demonstrates Tolkien's mistake when he assumed that the year had the same length as the present era. Curiously, the resulting dates are close to those generated by the Gregorian calendar. Options for resolving this matter will be covered in part 8.
(*4) SOLEX is a program that calculates astronomical data using numerical integration, allowing for pinpoint accuracy even tens of thousands of years in the past (assuming times in Terrestrial Time). According to SOLEX the exact moment in Terrestrial Time is Julian -3103/01/26 14:40:02.5. For a comparison Bromberg's Kalendis puts the moon in question at 16:14 UT on -3104-12-30, around an hour earlier, due to the algorithms used there dropping off in accuracy 5000 years in the past. Also note that the standard error in DeltaT at the time was around 2 hours 40 minutes.
(*5) "The evening star had risen and was shining with white fire above the western woods." - p.357. 14 Solmath is per the Tale of Years in my copy, and evidently in James's copy as well. However, the text makes it clear that this occurred the day before the Fellowship departed, whereas the Tale of Years has a 2-day gap, and thus this was altered to the 15th in recent editions.5b: A mild digression: relating the Shire calendar in modern times
A number of sources have attempted to construct a correlation between the Shire Calendar and the Gregorian calendar for use with present-day dates. Since we can't ascertain what the correlation would be if the Shire calendar actually continued to the present day, we can only make educated guesses. For example:
Wikipedia:
Mid-Year's Day = 22 June in common years (approximate)
Encyclopedia of Arda:
Mid-Year's Day = 22 June in common years (not specified for leap years)
Shire-Reckoning: Mid-Year's Day = 21 June in common years, 20 June in
Gregorian leap years
Takahashi
I: Fix Mid-Year's Day to the summer solstice (21/20 June in modern times)
Takahashi II: 10 Afteryule = 1 January i.e. Mid-Year's Day = 21 June in
common years, 20 June in Gregorian leap years
Three Rings: Mid-Year's Day = 22 June in common years
Baker: Mid-Year's
Day = 21 June in common years, 20 June in leap years
Shapiro: does not address modern times, but allocates Mid-Year's Day = 23
June in common years, 22 June in leap years during the Third Age
Strom: Mid-Year's Day = 25 June in common years, 24 June in leap years
Zavalloni
based on Korablev:
1 Tuile = 25 March = 6 Astron i.e. Mid-Year's Day = 19 June
Almatolmen:
Mid-Year's Day = 23 June
Otaku-sempai:
Mid-Year's Day = 21 June in common years, 20 June in leap years
In short, the majority of people correlate 21 June in common years to Mid-Year's Day, consistent with the summer solstice in modern times as per Tolkien's statement, as well as his claim that dates were "some ten days" ahead of the Gregorian, when considered seasonally. A few correlate 23 June, following Tolkien's other statement that 1 January = 9 Afteryule, which seemingly contradicts his "ten days" earlier in the same sentence (under the 23 June correlation there are no months in which the dates differ by ten days), though one could argue that eight days is close enough to count as "some". Two outilers also exist; Strom used the schedule that Tolkien applied to his moon phases as a direct correlation, which isn't robust in the slightest. The person who quoted Korablev took his assumption that 1 Tuile = 25 March and applied it to the era of the Lord of the Rings. This is problematic since as shown in earlier sections of this article the Imladris calendar had been drifting relative to the human calendars for six or seven millennia, and so probably did not correspond to the equinox anymore by that point in time.
Part 6: How can we reconcile all this? - Moon phase errors
It is clear that not every issue raised on this page can be resolved solely by in-universe arguments, particularly the moon phase errors. S-R points out many such arguments that could be used to explain the 22 Solmath - 8 Rethe discrepancy, then refutes all of them. Thus, this can only be explained by an error in the text. The easiest way of correcting such an error is by having Pippin observe a full moon (instead of "almost at the full") on the night of 7/8 Rethe, which allows said moon to drift back by nine hours or more (to during the day of 7 Rethe) since the following new moon is also slightly early.(*6) Indeed, Tolkien's original version of the scene had Pippin observing the almost full moon at around 9pm on 7 Rethe rather than early on 8 Rethe. It is likely that the entire scheme can be shifted back without any new problems, though I have yet to check in detail.
As for the West Gate of Moria? S-R implicitly moves the events to after midnight, which doesn't really tally with the dialogue after they enter the gate. I, personally, am tempted to claim that the gate actually faced south, which would mean that the moon could shine on it even when it was rising. I have no idea how plausible this would be, especially given that it's on the east bank of a lake.
What of the moon phase errors between The Hobbit and LoTR? Möhn attempts to explain this by assuming a different value of the mean synodic month, around 29.518 days. Back to Bromberg, whose graph tells us that the month was a mere 2 seconds longer in -7000, not nearly enough to make a difference (projected over 78 years gives about half an hour, whereas what is required is several days); a crude extrapolation finds that the lunar cycle's length in fact corresponds to about 4.7-5.1 million years in the future (not past, as asserted by Gamling and Strom, who have both forgotten about the change in the length of the day). Even if we accept Belyakov's figure of 205000 years in the future (the calculations for which are unknown) it is clear that this explanation is not viable. Trying to adjust the month length by going millions of years in the opposite direction is equally futile, given the content of parts 4 and 5.
Strom attempts to reconcile the moon phase errors in The Hobbit by moving the events backwards one year. This is, of course, problematic since the time interval is referenced (directly or indirectly) no less than four times (once in the Prologue, once in Chapter 1 when Bilbo mentions his 51st birthday, at least once in Appendix A and of course once in Appendix B), not to mention the fact that Frodo explicitly departs Hobbiton on his 50th birthday, wanting to leave at the same age as when Bilbo began his journey, and the age difference between Frodo and Bilbo is a plot point (and therefore cannot be altered). Finally, this only accounts for 11 or 12 days of the error, so his midsummer's eve moon turns out to be slightly too old (7 days or so - details in part 7).
Rather than that, I will consider in detail an alternate theory, namely that there are errors in the text of The Hobbit (if you insist on a Watsonian explanation, either in the copy of the Red Book Tolkien purportedly had or in translation), and that the moon on 1 Lithe really was 19 days old.
(*6) Based on the NASA table of moon phases for 1942, the full moon corresponding to that of 7/8 Rethe occurred at 00:20 UTC, so Pippin should have seen a full moon anyway. The new moon corresponding to 22 Solmath occurred at 10:03 UTC, so under this proposal both would still need to be shifted back.
Part 7: A tangent - a novel dating scheme for The Hobbit
This section is devoted to constructing a plausible chronology for The Hobbit under the assumption that the date of Durin's Day is consistent with the moon phases of The Lord of the Rings. The convenience of this is that ending autumn on Blotmath 14 is consistent with a solar insolation definition of the seasons, and no retcons need to be made to any part of the Lord of the Rings (we know that Tolkien was intending to revise The Hobbit in 1960 anyway, courtesy of The History of the Hobbit - some of his notes quoted there, incidentally, assume a 28-day lunar cycle, further proof Tolkien's astronomy knowledge runs the full gamut from "sublimely accurate to agonizingly incorrect", to quote Larsen).
--But hang on. What is Durin's Day anyway?
7a: How exactly is Durin's Day defined?
There seems to be some confusion as to exactly what Durin's Day is supposed to be. In particular, it has a tendency to be conflated with the Dwarves' New Year, which is defined as the first day of the last moon of autumn. Such a mistake is performed by Möhn, for example, when he asserts that it would have been trivial for Elrond to predict Durin's Day; others have shown that this is clearly not the case. Conversely, some people, such as Iduna, assume that any day during the last moon of autumn where the moon and sun can be seen together could be a Durin's Day, and take the first such day as Durin's Day.
However, if one reads the text carefully, it is clear that both are distinct events, and in turn Thorin mentioning the Dwarves' New Year in relation to Durin's Day strongly implies that Durin's Day is a dwarven new year on which the moon and sun can be seen together. This is the definition taken by most authoritative sources (e.g. Tolkien Gateway, Encyclopedia of Arda). It follows also that not all years contain a Durin's Day.
So, one needs to combine the first day of a moon with the lunar crescent being visible at sunset. The question remains: how is the first day of a "moon" defined in the dwarven calendar? The first option is the astronomical full moon, in other words the conjunction of moon and sun. This would imply that at sunset on that day the moon would be less than 24 hours old (18 hours if days begin at midnight, 12 hours if days begin at sunrise). Calculating whether the crescent moon is visible is a surprisingly non-trivial task, especially when considering the first visible lunar crescent. There have been many studies of whether it is possible for the moon to be visible if it was less than 24 hours old; the conclusion is that this is possible but heavily dependent on various factors relating to the position of the moon. Whether the moon would also be visible before sunset is something that is generally not addressed; Hunnewell cites Schaefer who claims that a separation of 35 degrees is necessary, and applies personal observations to conclude that somewhere between 18 and 24 degrees is needed. I tried myself in Stellarium, and found viewing the moon both at and after sunset to be nearly impossible for me at 24 hours, even when conditions were favourable (e.g. on 19 February 2015 in New York, when it should be visible excluding light pollution). However, I noted that the glare from the sun did indeed make it harder to view the moon at somewhat later times.
The other option is the first visible lunar crescent - that is, the day on which the lunar crescent is first seen is declared to be the first day of the month. This has precedent in the Islamic calendar, as well as the Karaite version of the Hebrew calendar. Indeed, since clearly Durin's Day is associated with the first visible lunar crescent and it is entirely possible that the dwarves were able to see it after sunset but not before, the definition fits what we know from the book.
Thus, here is my definition of Durin's Day, as a list of criteria that need to be satisfied:
- Previous (astronomical) new moon falls during dwarven autumn
- Next new moon falls during dwarven winter
- On the previous day, the lunar crescent is not visible
- On Durin's Day, the lunar crescent is visible before sunset
There is no definition of dwarven autumn supplied anywhere in Tolkien's writings. Many have tried to substitute various definitions; for example, if autumn is held to end at the winter solstice then the Dwarves' New Year would fall in November or December. However, this is unlikely to be the dwarves' definition for various reasons, most notably because this would only give a little over a month between Durin's Day and the return to Beorn's. More likely, the Dwarves' New Year would fall earlier than this.
7b: When is Durin's Day in The Hobbit?
In the past some people have proposed various dates for Durin's Day. Quite a few of those have been extended to full chronologies, which are featured in part 7c. In particular, the most-cited examples are Fonstad (The Atlas of Middle-earth) who puts Durin's Day on 30 Winterfilth, and Möhn who puts it on the 22nd. Tolkien's notes in the 1960s put Durin's Day firstly on the 17th and then on the 19th.
As for the proposals I haven't tabulated, Larsen's essay from The Hobbit and Tolkien's Mythology (2014) mentions articles by Schaefer (1994) and Hunnewell (1999), which I don't have access to, in addition to the below-tabulated Fonstad, Möhn and Harder; a post by Schaefer elsewhere gives the date as 3 November (calendar not specified), while Hunnewell's essay in the same compilation suggests a date of October 30, which may be the same as in the 1999 essay cited by Larsen. This last date corresponds quite closely to my 8 Blotmath when converted, which is slightly surprising given that it was derived using a different method. Otaku-sempai goes through a few iterations before eventually arriving at 22 Winterfilth, based on the last week of autumn and midsummer's eve. Graham Lockwood posits "November 10th" which appears to refer to 10 Blotmath, based on the last week of autumn; Almatomen uses similar logic to reach 23 Winterfilth.
As for me? My definition of Durin's Day if combined with the lunar ephemeris for 1864 gives exactly one possibility: 8 Blotmath. The new moon would have occurred on the 6th, corresponding to 31 October 1864; on the following day a check using Moontool or similar shows that the moon would not be visible in the region of the Lonely Mountain (central Europe). Thus, 8 Blotmath is the first day on which the moon is visible, and since the moon is nearly two days old it would be visible at sunset. Of course, none of this accounts for any lunar shifting from that year that might take place.
Given these comments, one can add this postulate to the above four:
- Dwarven winter in S.R.1341 begins on or around 15 Winterfilth.
As mentioned above, this is consistent with placing the end of autumn and the beginning of winter halfway between the autumn equinox and the winter solstice.
7c: The chronology proper
Let's go through the implication of putting Durin's Day on 8 Blotmath.
Firstly, either the date, the time or the moon phase of the moon-rune reading would need to be changed. Since the moon on 1 Lithe is now a waning gibbous, it can only rise after midnight; furthermore, keeping it on that date would require changing the nature of the moon under which the moon runes were read. Otherwise, let's say that the date is wrong (blame Bilbo's faulty memory, perhaps?), and the runes were read about two weeks earlier, say 17 Forelithe. Given that the party spent weeks at Rivendell it's highly likely that they arrived before this date (see also the dating schemes below). In fact, is it really plausible that Elrond would only decide to look at the map on the last night of their stay, given that Gandalf would surely have explained the purpose of their journey fairly early on?
Secondly, this would imply that the party spent at least three weeks waiting for Durin's Day. Given that they need a number of days to search for the door, this may not be a problem (Tolkien considered his estimate of 12 days short but doable; this would be long but plausible).
Thirdly, on the night of 1/2 Thrimidge 1342 Bilbo woke to the moon close to dawn. Taking the moon phases of 1865 gives a new moon on that date. Can we fix this? Well, to fix the moon one would need to shift the phase by at least one day. Alternatively we can alter the date (yes, again - save your complaints until the end) by a few days, allowing Bilbo to wake to the rising moon. Until I work out whether shifting the phase while shifting other dates is possible I'll assume the second option.
Fourthly, does everything else still match? To answer this question, here's a table comparing some of the different dating schemes that have been proposed for The Hobbit, including my proposed dating scheme:
| 1991 | 1999-2001 | 2003 | 2009 | 2011 | 2012 | 2013 | 2015 | ||
|---|---|---|---|---|---|---|---|---|---|
| Event | Fonstad | Möhn | Belyakov | Harder | Auraran | Gamling | JtJ | Proposed | Notes |
| Gandalf meets Bilbo | 25 Ast | 25 Ast | 25 Ast | 26 Apr | 25 Apr | 25 Ast | 25 Ast | 25 Ast | A "Tuesday" |
| The unexpected party | 26 Ast | 26 Ast | 26 Ast | 27 Apr | 26 Apr | 26 Ast | 26 Ast | 26 Ast | Given in semi-canonical sources (Quest for Erebor) |
| Leaving Hobbiton | 27 Ast | 27 Ast | 27 Ast | 28 Apr | 27 Apr | 27 Ast | 27 Ast | 27 Ast | Next day |
| The Stone-trolls | 29 Thr | ~29 Thr | 29 Thr | 25 May | 25 May | 23-25 Thr | 29 Thr | ~29 Thr | "Wandering" moon appears around sunset – Harder claims it was waning (1st ed?) |
| Arrival in Rivendell | 4 Fol | ~15 Fol | 7 Fol | 29 May | 5 Jun | ~1-5 Fol | 4 Fol | ~4 Fol | "The light became dim, for the moon had not risen" |
| Elrond reads the moon-runes | 1 Lit | 1 Lit | 1 Lit | 20 Jun | 23 Jun | 1 Afl | 1 Lit | ~17 Fol | A "broad silver crescent" in the evening on midsummer's eve (implies waxing, which is ignored by Harder and Auraran; midsummer's eve ignored by proposed) |
| Leaving Rivendell | MYD | MYD | MYD | 21 Jun | 24 Jun | 2 Afl | MYD | MYD | Over 2 weeks, stated to be "Midsummer's day", estimated by Tolkien as 24 Jun (Rateliff) |
| Captured in Goblin-town | 16 Afl | 9 Afl | 16 Afl | 4-5 Jul | 10 Jul | 9 Afl | 16 Afl | 16 Afl | A "Monday" |
| Escape from Goblin-town. Eagle rescue. | 19 Afl | 12 Afl | 19 Afl | 7 Jul | 13 Jul | 12 Afl | 19 Afl | 19 Afl | A "Thursday". Moon shining into clearing during night, rose fairly early |
| Arrival in Beorn's Hall | 20 Afl | 13 Afl | 20 Afl | 8 Jul | 14 Jul | 13 Afl | 20 Afl | 20 Afl | Next day |
| leaving Beorn | 22 Afl | 15 Afl | 22 Afl | 10 Jul | 16 Jul | 15 Afl | 22 Afl | 22 Afl | 2 days |
| Edge of Mirkwood; Gandalf departs | 25 Afl | 18 Afl | 25 Afl | 13 Jul | 20 Jul | 19 Afl | 25 Afl | 25 Afl | "Fourth day" |
| Enchanted stream crossed | 16 Wed | ?? Wed | 8 Wed | 31 Jul | 28 Jul | ?? Wed | 16 Wed | 16 Wed | |
| Bilbo rescues Dwarves | 23 Wed | ?? Wed | 16 Wed | 7 Aug | 2 Aug | ?? Wed | 23 Wed | 23 Wed | Seven days afterward |
| Imprisoned by the Silvan Elves | 24 Wed | Late Wed | 17 Wed | 8 Aug | 3 Aug | Late Wed | 24 Wed | 24 Wed | Next day |
| Escape from Thranduil's Halls | 21 Hal | 21 Hal | 21 Hal | 20 Sep | 20 Sep | 21 Hal | 21 Hal | 21 Hal | |
| Arrival in Lake-town; Bilbo's birthday. | 22 Hal | 22 Hal | 22 Hal | 22 Sep | 22 Sep | 22 Hal | 22 Hal | 22 Hal | Given in LotR |
| Thorin begins to think of leaving | 6 Win | 6 Win | 6 Win | 6 Oct | 6 Oct | 6 Win | 6 Win | 6 Win | 2 weeks |
| Departure from Lake-town | 9 Win | ~8 Win | 9 Win | 7 Oct | 9 Oct | ?? Win | 9 Win | 9 Win | |
| fourth day after leaving; camp at Ravenhill | 13 Win | ~12 Win | 13 Win | 11 Oct | ~12 Oct | ?? Win | ~13 Win | 13 Win | 4 days |
| Bilbo discovers the hidden path | 19 Win | ?? Win | 9? Blo | 18 Oct | 20 Oct | ?? Win/Blo | ?? Win | ~1 Blo | |
| Durin's Day, first day of "the last week of autumn" | 30 Win | 22 Win | 11 Blo | 24 Oct | 25 Oct | 7 Blo | 20 Win | 8 Blo | Visible crescent moon, estimated by Tolkien as ~17 or ~19 Win in Rateliff |
| Death of Smaug | 1 Blo | 23 Win | 12 Blo | 25 Oct | 26 Oct | 8 Blo | 21 Win | 9 Blo | Next day; impossible rising waxing moon |
| Elves set out; Roäc informs Thorin of Smaug's death | 3 Blo | 26 Win | 14 Blo | 28 Oct | 29 Oct | 10 Blo | 23 Win | 12 Blo | Smaug's death the "third night back" |
| Elves arrive at Lake-town | 6 Blo | 28 Win | 17 Blo | 30 Oct | 31 Oct | 13 Blo | 26 Win | 15 Blo | |
| Elves and Men set out for Erebor | 12 Blo | 4 Blo | 23 Blo | 5 Nov | 5 Nov | 15 Blo | (7 Blo) | 20 Blo | "eleven days from the ruin of the town" |
| Elves and Men in Dale. Scouts examine Erebor | 15 Blo | 7 Blo | 24 Blo | 8 Nov | ?? Nov | 22 Blo | 5 Blo | 24 Blo | |
| Thorin rejects the claims of Bard and Thranduil | 16 Blo | 8 Blo | 26 Blo | 10 Nov | ?? Nov | ?? Blo | ?? Blo | 25 Blo | |
| Bilbo gives away the Arkenstone | 22 Blo | ?? Blo | 8 Foy | 16 Nov | 23 Nov | 27 Blo | 12 Blo | ~29 Blo | "black and moonless" early in the night |
| Battle of the Five Armies | 23 Blo | Mid Blo | 10 Foy | 18 Nov | 25 Nov | 29 Blo | 13 Blo | ~1 Foy | Two days later |
| Leaving Erebor | 27 Blo | Late Blo | 14 Foy | 25 Nov | ?? Nov/Dec | ?? Foy | 17 Blo | ~5 Foy | |
| Arrival at Beorn's Hall | 30 Foy | ~30 Foy | 1 Yul | 20 Dec | 21 Dec | 30 Foy | 30 Foy | 30 Foy | |
| Return to Rivendell | 1 Thr | 1 Thr | 1 Thr | 1 May | 1 May | 1 Thr | 1 Thr | ~25 Ast | Stated to be "May 1st", moon shining through a window in late night (retconned in proposed) |
| Return to Hobbiton | 22 Fol | (22 Fol) | 22 Fol | 22 Jun | 22 Jun | 22 Fol | 30 Fol | 22 Fol | Stated to be "June 22nd" |
Bracketed dates are dates that can be calculated from known dates and the original book, but were not supplied in the source chronology. Question marks mark unknown dates that cannot be calculated.
And while we're at it, let's put in a table of the new moons for each dating scheme (except Fonstad):
| Month | Möhn | Harder | Belyakov | Auraran (1995) | JtJ (1863) | Gamling/Proposed (1864) | JtJ (-4086) |
| 4 | 26 Ast | ~30 Apr | ~14 Ast | 29 Apr L | 25 Ast E | 12 Ast L | 26 Ast L |
| 5 | 25 Thr | 29 May | ~14 Thr | 29 May E | 24 Thr L | 11-12 Thr | 26 Thr E |
| 6 | 25 Fol | 28 Jun | 13 Fol | 28 Jun MN | 24 Fol E | 11 Fol M | 25 Fol L |
| 7 | 21 Afl | 27 Jul | 10 Afl | 27 Jul L | 19 Afl L | 7-8 Afl MN | 20 Afl L |
| 8 | 21 Wed | 26 Aug | ~10 Wed | 26 Aug E | 18 Wed L | 7 Wed L | 20 Wed E |
| 9 | 20 Hal | 24 Sep | ~9 Hal | 24 Sep L | 18 Hal E | 7 Hal E | 19 Hal L |
| 10 | 20 Win | 24 Oct | ~9 Win | 24 Oct E | 17 Win L | 6 Win L | 19 Win E |
| 11 | 19 Blo | 23 Nov | 8 Blo | 22 Nov L | 17 Blo E | 6 Blo L | 18 Blo L |
| 12 | 19 Foy | 22 Dec | 8 Foy | 22 Dec E | 16 Foy L | 6 Foy E | 18 Foy M |
A few key points on each dating:
- Fonstad, by her own admission, can't calculate moons at all; her 30 Winterfilth matches nothing whatsoever (the implied midsummer's eve moon is a waxing gibbous). She can, however, calculate travel times (explaining why James decided to use her solution as a base), and at least knows her way around the Shire calendar.
- As mentioned above, Möhn started from the midsummer's eve moon and extrapolated Durin's Day on 22 Winterfilth. He allows around 15 days to travel from the Trollshaws to Rivendell, which is considerably longer than the other schemes, especially given the relatively short distance.
- Belyakov assumes the moons from the Lord of the Rings, although his calculations give moon phases slightly later than the correlation used by myself and Gamling. He makes no attempt to reconcile the moon phase on 1 Lithe. In addition, his date for the Battle of the Five Armies is the latest of all the chronologies here, leaving a mere 17 days to travel from Erebor to Beorn's house.
- Harder uses the Gregorian calendar (or something with the same month structure), using as his justification the line addressed in part 2c. He fixes Midsummer's Day on either the 20th or 21st, which is the same as in modern times, and takes winter to begin on 1 November but puts Durin's Day one day early, on 24 October, which contains an astronomical new moon. I seriously doubt his moon would be visible at all on that day, let alone at sunset. His Midsummer's eve contains a waning crescent instead of waxing; I suspect Elrond, Gandalf and co. wouldn't have stayed up that late, though I could be wrong.
- Auraran does the same, without justification. He takes winter to begin on 1 November, thus putting Durin's Day on 25 October. His calculations find that the moons correspond to those of 1995, which are provided in the table.
- Gamling starts from the Lord of the Rings date, as I have. However, he assumes that the summer solstice fell on 2 Afterlithe instead of Mid-Year's Day. Given the results attained above this at first seems somewhat plausible; however, Aragorn and Arwen's wedding fell on Midsummer's Day which was also on Mid-Year's Day, and so combined with the earlier assumptions (noting that Mid-Year's Day would have been a few days off) the assertion starts to become problematic. Incidentally, the adjustments in the Gondorian calendar cannot be used to explain this because the difference is in the wrong direction. Most of the rest of his solution is based on Möhn.
- Strom modifies Fonstad's dating to give his own, based on a Durin's Day of 20 Winterfilth... except that if one looks at the above table one finds that the moon (based on the corrected correlation for -4086, two days earlier than the one he provided) was 4 days old at that time, which means that Durin's Day would be at least one day earlier. Furthermore, checking the moon age on 1 Lithe gives over 7 days, enough for it to be considered at first quarter! Guess he'll have to try again.
- As mentioned earlier, my solution was designed starting from the Lord of the Rings date, and thus has no implicit retcons of that work, the implications of which have already been discussed. Conversely, it has major retcons of dates in The Hobbit. Most of my solution is based on Fonstad with alterations based on Auraran and for the later Durin's Day; it was constructed independently from Belyakov's and Gamling's.
You may notice also that some dates in the past chronologies don't seem to match the periods mentioned in the notes. In a later version I'll detail exactly where the mistakes are, but at the moment you can check for yourself. All such errors should have been eliminated from the proposed chronology (retcons are, of course, a different matter).
Part 8: Resuming where we left off: Year length errors
As for the year length errors? Well, as calculated in part 5, using the summer solstice as a reference point gives an average year length of between 365.243135 and 365.244056 days from II.1 to III.3021. Considering that the Númenorean calendar assumed a year length of 365.242 days and that this was presumably calculated between II.1 and II.1000, the fact is that something has clearly gone wrong.
So, let's consider the various sources of variation in the values given here. Firstly, the change in the length of the day. This was already addressed in part 4 and 5, so not much else can be said, except that XKCD What If? has already discussed just how much is needed to negate the slowing over merely the past 200 years. Secondly, changes in Earth's orbit. Suffice to say, one needs a pretty large object to send the Earth's position millions of kilometres off course, even after thousands of years. For example, JPL's ephemerides give a possible error on the order of hundreds of kilometres, albeit for the period -3000 to +3000. This is significantly less than the error created by DeltaT in that timeframe (at least at the edges).
It is clear, then, that one needs a pretty significant event to fix this internally, one that would be cataclysmic and world-altering in its magnitude. With this in mind, let's assume that Möhn was wrong about the Downfall of Númenor not affecting the millennial deficits, and consider how much the length of the year would have to be affected to fix the solstice timings.
In short, the period between the summer solstice of II.1 and that of III.2060 would need to be 8-9 days shorter. Using the JtJ analysis and assuming that the solstice of II.1 fell exactly 8 days later than that calculated above, while the solstice of II.3319 is accurate, one calculates the revised mean year length from II.1 to II.3319 to be 365.24154 days, assuming that the moment of solstice in II.1 was exactly 8 days later than that calculated in part 5. This is just close enough to 365.2422 that the Númenorean leap rule is now plausible, and the rest follows once one assumes that no-one bothered to check what was going on with the year length for two millennia or so.
Part 9: Conclusions
Over the course of this article I have made a pretty exhaustive analysis of the astronomical errors that Tolkien made while writing his legendarium. We've established that Tolkien, despite his boasts about consistency, is just as prone to making errors as any of us. In particular:
- Tolkien can't calculate moons within a single year, let alone a range of two years, let alone 78, let alone thousands;
- The year was most certainly not the same length as it is now, but the whole thing works out due to pure luck;
- Every attempt to create a chronology of The Hobbit is flawed, and creating one without retconning The Lord of the Rings requires multiple retcons of the Hobbit (but if his notes from 1960 are any indication Tolkien knew that already);
and so on. However, probably a more important observation is that those who've tried to analyse his work are also prone to errors, even with modern freely available knowledge; such errors have ranged from minor typos to glaring holes. (Of course, this article is no exception, hence the many revisions, though the original analysis should be sound, at least.) Moreover, there is also a tendency to overlook relevant past analyses for a variety of reasons, usually because the writer is unaware of the existence of the work in question. Again, this analysis has attempted to avoid this by incorporating as much relevant past analysis as possible. Thus, let this be a lesson to those who come after.
Appendix: Links
Most of the links have been included inline in the text. For those sites referred to multiple times in the text, I give links below.
Three Rings: http://3rings.webs.com/chronology,
updated with a calendar page http://3rings.webs.com/calendars
in 2014
Lalaith's Middle-earth Science Pages (Andreas Möhn) (currently dead as of
2016-02-29): http://homepage.o2mail.de/lalaith/M-earth.html
- much of his past material has been moved to non-free ebooks
old version: https://web.archive.org/web/20120211150227/http://lalaith.vpsurf.de/Tolkien/Time.html,
https://web.archive.org/web/20120211145842/http://lalaith.vpsurf.de/Tolkien/Durin%27s_Day.html
even older site: https://web.archive.org/web/19990502060419/http://rover.wiesbaden.netsurf.de/~lalaith/Tolkien/Durin%27s_Day.html
Shapiro: http://www.elvish.org/gwaith/calendars.htm
Shire-Reckoning: http://shire-reckoning.com/faq.html
Monteiro: http://www.oocities.org/albmont/medating.htm,
http://www.oocities.org/albmont/mecalend.htm
(date differences)
Heirs of Durin: http://thorinoakenshield.net/tag/durins-day/
- two articles on Durin's Day, one with a link compendium
Annals of Ennor: http://lostworldofennor.angelcities.com/time.htm
- a somewhat spurious source
James the Just: http://tolkienforums.activeboard.com/t42820320/middle-earth-chronology/,
http://tolkienforums.activeboard.com/t53584608/a-chronology-of-the-hobbit/,
http://tolkienforums.activeboard.com/t55579915/imladris-calendar/
Bromberg: http://individual.utoronto.ca/kalendis/seasons.htm
In addition, links to a few other relevant websites have been provided:
https://wcpltn.wordpress.com/2014/10/21/its-durins-day/
- argument for an "early" (as opposed to December) Durin's Day
http://web.archive.org/web/20040501112831/http://www.geocities.com/otsoandor/Concordance.htm
- compact concordance
http://lumeardaron.mariot.me.uk/
- today's date, using Shapiro correlations
http://realelvish.net/greatyears.php
- alternate source for Fonstad
http://lotrproject.com/ - a nice
timeline
http://www.physics.ccsu.edu/Larsen/astronomy_of_middle.htm
Robert H. van Gent on DeltaT: http://www.staff.science.uu.nl/~gent0113/deltat/deltat.htm